Last couple weeks I added a lot of documentation, implemented important tests and fixed couple minor bugs, so this post is the summary for my implementation of primality test algorithm during GSoC with flint.
APR-CL is the mostly used algorithm for proving primality of general numbers. APR-CL (Adleman, Pomerance, Rumely, Cohen, Lenstra) is the modification of APR test. There are several versions of this algorithm and my implementation mostly described in [1] and [2]. Other modern tests are ECPP (Eliptice curve primality proving) and AKS (Agrawal–Kayal–Saxena).
APR-CL test uses the idea that we can not only check some conditions, but also collect this information and finally say that the number doesn't have any non trivial divisors. APR-CL uses the congruents analogues to Ferma's one. Finally, after we check some of these tests we can see that all possible divisor of n in small set of numbers, and to check that number is prime we only need "several" divisions ("several" can mean millions of divisions...but it's not very much for the numbers with thousands of digits). For more information see previous posts: (1), (2), (3).
My implementation is mostly based on [1]. I implemented a simple version that does not use $p-1$, $p+1$ or Lucas style tests. While codeing I looked at PARI/GP and mpz_aprcl implementations and took some initial values (t's) from PARI. After that I spent some time for "tuning" and now I believe that I chose a good values for numbers up to 2000 digits (but perhaps they can still be improved).
So, the algorithm consists from three steps:
As before, $n$ is the number to test for primality. We have $s$ such that $s^2 > n$ and $gcd(s*R, n) = 1$ and $a^R \equiv 1 \mod{s}$ for all $a$ coprime to $s$. Here we have 2 goals: minimize the $s$ and minimize the cost of future Jacobi sum test for $s$ divisors. I implemented only the first but the second also requires research (some ideas are described in [3]). Next we have final division step which depends from size of $R$ value. In final division we need to do $R$ divisions and it takes meaningful amount of time for big $n$.
$s$ reduction step described in this post. Also we can select $s^3 > n$, in all papers it was given as important improvement, but not implemented. Using flint implementation of Divisors in Residue Classes algorithm I have not get any speed gain for tested numbers. So I did not use it.
The essential part of Jacobi test step is to verify that power of multiplication of Jacobi sums is the unity root. So, the longest part of this step is exponentiation. As before we represent Jacobi sums as poly modulo cyclotomic poly, so we need to optimize modular polynomial exponentiation. This can be done in two directions: optimize powering function or polynomial multiplication/squaring functions. I worked on both of this and implemented 2^k-ry, sliding window exponentiation methods and special functions for multiplication and squaring.
In the future, this step can be improved if we add more special mul/sqr function (which, I believe, can be builded automatically, if we use some optimization methods..). Also before this step we can use Lucas style tests to look at some divisors and exclude them from Jacobi test. Finally, we can use some special forms of number to reduce the number of divisions (mod operations). For example, Montgomery form was implemented and tested, but it not give any speed up. I think it was mostly because I not implement it accuracy and better implementation can give some speed boost.
Some of these and other concepts are described [3].
In final step we just need to verify that n is prime. It was not very possible that we verify that n composite in this step, so it can't be used as effective factorization algorithm. In this step we know that all possible divisors of n can be find: if $s^2 > n$ then we check dividers in the form $n^i \mod{s}$; if $s^3 > n$ then we use Divisors in Residue Classes algorithm.
One of the easy and possible things to do is parallelization of second and third steps. I think it gave near linear speed up from number of processors, while we have only data ($q$ values in second and divisions in third) dependency which easy divides.
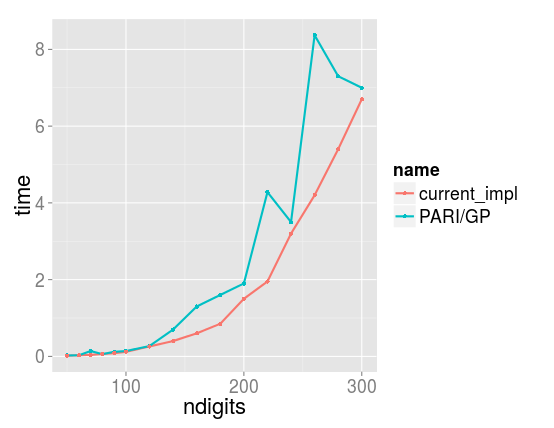
Finally I provide timings for current version. It can prove primality of 100 digit number for 0.7, 300 digit for 4 and 2000 digit for one hour on my 2.7 GHz Core i5 processor.
So, I think it have good timings and believe it was many possible improvements. I hope my code was usefull for flint and merged after all necessary corrections.
Also provides Gauss sum test described in [4], which is not very useful in practice, but can beuseful for people who want to see an implementation of these.
Thanks flint and Google for this great summer of code!
[1] - "Implementation of a New Primality Test" by H. Cohen and A. K. Lenstra
[2] - "A Course in Computational Algebraic" by H. Cohen
[3] - "PRIMALITY PROVING WITH CYCLOTOMY" by Wiebren Bosma
[4] - "Four primality testing algorithms" by René Schoof
APR-CL is the mostly used algorithm for proving primality of general numbers. APR-CL (Adleman, Pomerance, Rumely, Cohen, Lenstra) is the modification of APR test. There are several versions of this algorithm and my implementation mostly described in [1] and [2]. Other modern tests are ECPP (Eliptice curve primality proving) and AKS (Agrawal–Kayal–Saxena).
APR-CL test uses the idea that we can not only check some conditions, but also collect this information and finally say that the number doesn't have any non trivial divisors. APR-CL uses the congruents analogues to Ferma's one. Finally, after we check some of these tests we can see that all possible divisor of n in small set of numbers, and to check that number is prime we only need "several" divisions ("several" can mean millions of divisions...but it's not very much for the numbers with thousands of digits). For more information see previous posts: (1), (2), (3).
My implementation is mostly based on [1]. I implemented a simple version that does not use $p-1$, $p+1$ or Lucas style tests. While codeing I looked at PARI/GP and mpz_aprcl implementations and took some initial values (t's) from PARI. After that I spent some time for "tuning" and now I believe that I chose a good values for numbers up to 2000 digits (but perhaps they can still be improved).
So, the algorithm consists from three steps:
- $R$ and $s$ selection
- Jacobi sum test
- Final division
As before, $n$ is the number to test for primality. We have $s$ such that $s^2 > n$ and $gcd(s*R, n) = 1$ and $a^R \equiv 1 \mod{s}$ for all $a$ coprime to $s$. Here we have 2 goals: minimize the $s$ and minimize the cost of future Jacobi sum test for $s$ divisors. I implemented only the first but the second also requires research (some ideas are described in [3]). Next we have final division step which depends from size of $R$ value. In final division we need to do $R$ divisions and it takes meaningful amount of time for big $n$.
$s$ reduction step described in this post. Also we can select $s^3 > n$, in all papers it was given as important improvement, but not implemented. Using flint implementation of Divisors in Residue Classes algorithm I have not get any speed gain for tested numbers. So I did not use it.
The essential part of Jacobi test step is to verify that power of multiplication of Jacobi sums is the unity root. So, the longest part of this step is exponentiation. As before we represent Jacobi sums as poly modulo cyclotomic poly, so we need to optimize modular polynomial exponentiation. This can be done in two directions: optimize powering function or polynomial multiplication/squaring functions. I worked on both of this and implemented 2^k-ry, sliding window exponentiation methods and special functions for multiplication and squaring.
In the future, this step can be improved if we add more special mul/sqr function (which, I believe, can be builded automatically, if we use some optimization methods..). Also before this step we can use Lucas style tests to look at some divisors and exclude them from Jacobi test. Finally, we can use some special forms of number to reduce the number of divisions (mod operations). For example, Montgomery form was implemented and tested, but it not give any speed up. I think it was mostly because I not implement it accuracy and better implementation can give some speed boost.
Some of these and other concepts are described [3].
In final step we just need to verify that n is prime. It was not very possible that we verify that n composite in this step, so it can't be used as effective factorization algorithm. In this step we know that all possible divisors of n can be find: if $s^2 > n$ then we check dividers in the form $n^i \mod{s}$; if $s^3 > n$ then we use Divisors in Residue Classes algorithm.
One of the easy and possible things to do is parallelization of second and third steps. I think it gave near linear speed up from number of processors, while we have only data ($q$ values in second and divisions in third) dependency which easy divides.
 |
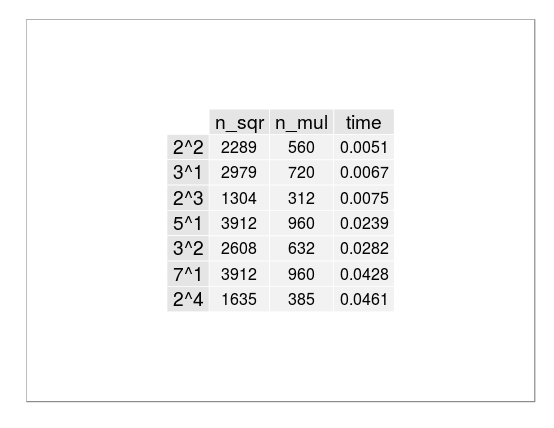
| from 50 to 300 digit numbers |
 |
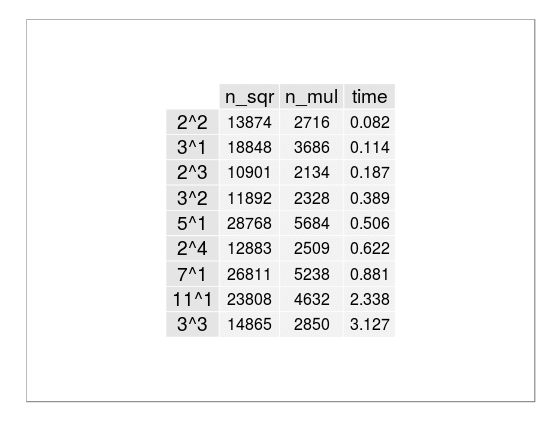
| from 300 to 2000 digit numbers |
Also provides Gauss sum test described in [4], which is not very useful in practice, but can beuseful for people who want to see an implementation of these.
[1] - "Implementation of a New Primality Test" by H. Cohen and A. K. Lenstra
[2] - "A Course in Computational Algebraic" by H. Cohen
[3] - "PRIMALITY PROVING WITH CYCLOTOMY" by Wiebren Bosma
[4] - "Four primality testing algorithms" by René Schoof