GSoC week 5; Some optimizations

This week I was working on the Jacobi sum test optimizations described in the last post.
First I add some fixed optimal $R$ values for $n$ with different number of digits. I also rewrite $s$ computation. This functions can be find here. It gave a good gain in speed, but I can add more intermediate $R$ values. It must be done carefully, because with smaller $R$ we can have worse $s$. This is shown in the graph, the PARI/GP implementation has many peaks.

mean time in seconds

Next I add $2^k$-ary powering algorithm. It gave ~20% gain in speed.

Also I do a lot of profiling using valgrind callgrind tool. I find that the computation of Jacobi sums takes a little time, so I'm not going to tabulate them.

I implement the final step of algorithm on condition that $s^3 > n$ using divisors in residue classes algorithm. After that all becomes slower. The divisors in residue classes algorithm have a good complexity $O((\ln n)^3$, but we need to call it thousands of times ($R = 2520$ for 100 digits $n$).

The next graph show timings for $n$ from 50 to 100 digits:

mean time in seconds

To better understand how selection of $R$ affects at the time I look at most slow part of algorithm ($n$-th powering in $\mathbb{Z}[\zeta_r] / (n)$) and count the number of operations. This can be seen in the following tables for 100 and 300 digits numbers: 
  
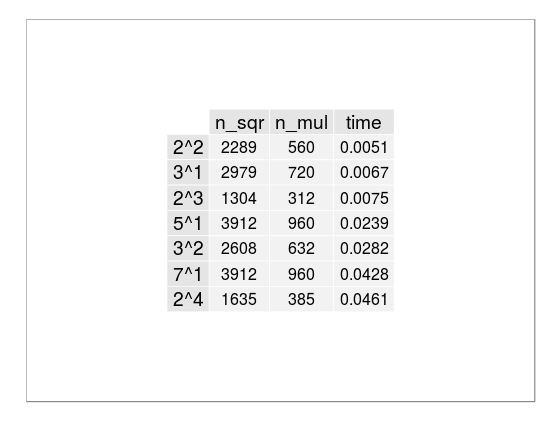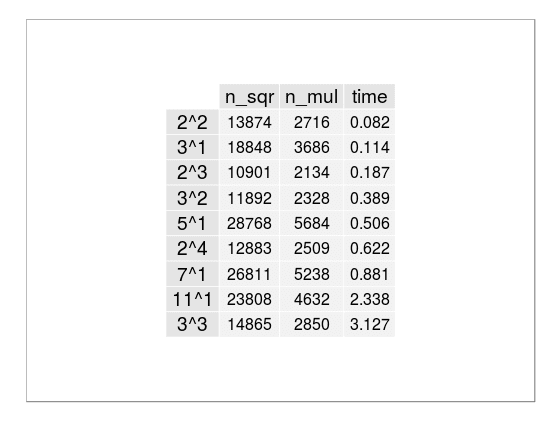Also attach link to valgrind outputs for 100 and 300 digits prime. 

Next I want try to use directly fmpz_vec operations, without fmpz_mod_poly abstraction. After this I want to implement some formulas described in "Implementation of a New Primality Test" for fixed $r = p^k$.

GSoC week 4; Jacobi sum test implementation and further optimizations

This week I implemented the basic version of Jacobi sum primality test. It is much faster then the test using Gauss sums. For example, primality proving of 50 digits prime using Gauss sum test takes ~200 seconds, and Jacobi sum test takes less then a second. The figure shows the number of up to 200 digits.

Implementation details are well described in "A Course in Computational Algebraic Number Theory" by H. Cohen and "Implementation of a New Primality Test" by H. Cohen and A. K. Lenstra. I also describe all the steps in code comments.

The image shows call graph output of valgrind --callgrind tool for 100 digits prime:

So, we can see that to improve the speed of algorithm we must reduce the number of multiplications (which are well optimized in flint).


Currently I have a very naive implementation of selecting $s$ and $R$ values (just trying increase $R = 2, 4, 6...$ until the proper $s$ is found). It can takes a lot of time and choose non-optimal parameters. For example, if we set $R = 98280$ it proves 200 digits number primality for ~8 seconds instead of 30. By $R = 166320$ we can prove 300 digits number in ~30 seconds. So I need to rewrite aprcl_config_init() function.

The next thing to do is replace the condition $s^2 > n$ to $s^3 > n$. Using "Divisors in Residue Classes" we can determine n divisors. It was implemented in flint before, so I need only add this step in Final division step.

Also I want to replace my basic powering algorithm in $\mathbb{Z}[\zeta] / (n)$ by $2^k$-ary method.

And finally we can precompute and store Jacobi sum in configuration structure (for 300 digits number computation of Jacobi sums takes ~40% of time) for testing numbers with a similar length.

This week I want to add this modifications and look in more detail the other opensource implementations.

GSoC week 3; Road to Jacobi sum test

This week there are two important results:

• Gauss sum test implemented and works;
• Written operations in $\mathbb{Z}[\zeta_{p^k}]$.

The Gauss sum implementation was tested and, as expected, it works slowly. Proof of primality of 50 digits number: $29927402397991286489627837734179186385188296382227$ takes near 200 seconds.

To speed up the algorithm can be used Jacobi sums instead of Gauss sums. The Jacobi sum $J(\chi_1, \chi_2)$ defined by: $$J(\chi_1, \chi_2) = \sum\limits_{x \in \mathbb{Z}/q\mathbb{Z}}{\chi_1(x)\chi_2(1-x)}$$ $J(\chi_1, \chi_2) \in \mathbb{Z}[\zeta_p]$, much smaller finite ring, so the computation is much faster. As before we represent elements of $\mathbb{Z}[\zeta_p]$ as $\mathbb{Z}[X]/(X^p-1)$. It was implemented multiplication, addition, memory management, powering and reduction modulo cyclotomic polynomial $\Phi_{p^k}(x) = \sum\limits_{i = 0}^{p - 1}{x^{ip^{m-1}}}$. All these operations are documented and tested.

I also implement computation of Jacobi sum as described in "Implementation of a New Primality Test" by H. Cohen and A.K. Lenstra.

This week I am going to finish simple version of Jacobi sum test. Then we can implement some optimizations described in "Implementation of a New Primality Test" and, maybe, think about the new.

GSoC week 2 and Gauss sums

As described earlier, we need to implement the operation in $\mathbb{Z}[\zeta_p, \zeta_q]$. We can represent $x$ from $\mathbb{Z}[\zeta_p, \zeta_q]$ as vector of size $p$ of $\mathbb{Z}[\zeta_q] = \mathbb{Z}[X]/(X^q-1)$. 

The addition of $x, y \in \mathbb{Z}[\zeta_p, \zeta_q]$ is just elementwise addition of polys $x[i] + y[i]$ for $i \in [0, p-1]$.
For multiplication $z = x * y$ from $\mathbb{Z}[\zeta_p, \zeta_q]$ we set
$$z[i +j\pmod{p}] \mathrel{+}= x[i]*y[j]\pmod{X^q-1} \text{ for } i,j<p$$

It will also be useful to have some memory management, comparison, powering and multiplication on $\zeta_p^k$ functions.

Now when we have structure to work with the elements of the $\mathbb{Z}[\zeta_p,\zeta_q]$ we can compute Gauss sum $\tau(\chi)$ for Dirichlet character $\chi_{p, q}$. $$\tau(\chi)=\sum\limits_{x \in (\mathbb{Z}/q\mathbb{Z})^*}{\chi(x)\zeta_q^x}=\sum\limits_{j=1}^{q-1}{\zeta_p^j\zeta_q^{g^j}}$$, there $g$ is the primitive root modulo $q$.

So, we now can compute Gauss sums. For test $n$ for primality we must check two conditions of the theorem 4.2 from "Four primality testing algorithms" for all $q$ and prime powers $r|q-1$:

• for every prime $t$ dividing $n$ there exists $t\lambda_t$ in the ring $\mathbb{Z}_l$ of $l$-adic integers such that: $$t^{l-1}=n^{(l-1)\lambda_t} \in \mathbb{Z}_l^*$$
• $\tau^{\sigma_n-n}(\chi)  \in \langle\zeta_p\rangle$ in the ring $\mathbb{Z}[\zeta_p, \zeta_q]/(n)$

$\tau^{\sigma_n}(\chi)=\tau(\chi^n)$, so the second condition can be checked as:
$$\tau(\chi^n)=\zeta_p^i*\tau^n(\chi) \text{ for some }i$$
The example how this works can be found in the unit-test for Gauss sum and in the Gauss sum primality test. 

The first condition  can be checked using Proposition 4.3 and Claim 2.

When I finally implement first condition the Gauss sum test will be finished and we can continue to implement APR-CL. In the beginning I need to rewrite operations in $\mathbb{Z}[\zeta_p]$ more carefully.