In the last week I tried a couple of interesting things, which well speed up the test.
Next following article, I have implemented the better $s$ reduction function (_jacobi_config_reduce_s2()) which is the approximation of knapsack problem solution. We choose weight of each $q$ equal to $w(q) = \sum\limits_{p | q-1}{\phi^2(p^j)}$, where $\phi$ denotes Euler's function. Then we find a prime power factor $q^k$ of $s$ with max $w(q)$ and set $s = s/q^k$. By doing this as long as possible, we will get a good $s$ value. It also gave a small speed boost. For better explanations and links you can look at chapter 4 of "Primality Testing and Jacobi Sums". As I see it is not implemented in PARI/GP aprcl.
I add config functions, which try to reduce $s$ value. If $s$ have prime power factor $q^k$ for which $s/q^k > n^{1/2}$ then we can choose biggest $q$ and set $s = s/q^k$. This is repeated until it is no longer possible (_jacobi_config_reduce_s()). It gave a nice speed boost for numbers $n$ which are much smaller than the computed number $s$. This optimization enabled us to slightly outperform PARI/GP and "smooth" time of computation (no spikes).
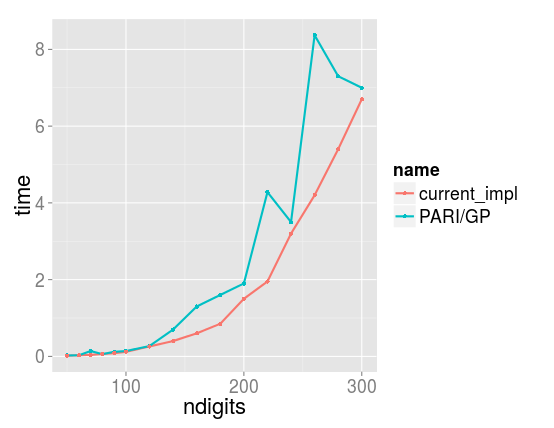 |
| up to 300 digits |
Another thing which gave interesting results - I remove $t = 166320 = 2^4*3^3*5*7*11$ and always use $t = 720720 = 2^4*3^2*5*7*11*13$. If we use it together with $s$ reduction function we have ~0.5 second speed up for 300 digits prime (5.6 sec instead of 6.1). These is because we do not have a special sqr/mul functions for p = 13 or p = 27, but for p = 27 we have poly of length 17 and for p = 13 length = 12. After using $s$ reduction function in both cases we have $s$ of similar size, but use faster multiplication/squaring. It works for all numbers which are used t = 166320. Also in this place there is space for optimization, because now in final divison step we need to do 720720 multiplications and divisions, and it takes ~15% of all time.
The next thing to look at in the future is special functions sqr/mul for all $p$ values. I look at p = 13 and write result for squaring and I don't think that's a good idea to work with it manually. It look like some type of cse task and I think I can find some algorithm for this later...
I also add special multiplication functions for p = 3, 4, 5, 7, 8, 9, 11 and 16. It gave just a couple of percent increase, but almost for free :)
So, now test works 0.115 sec for 100 and 5.6 sec for 300 digits numbers (I think I have never posted my processor type - Core2Duo T6670 2.2GHz processor, so I do not have avx instructuions set, which may be can be used in gmp).
This week I want to fix all warnings I have, do some refactoring and add more documentation. I also want to add something similar to profile folder with primes of different sizes (from https://primes.utm.edu/lists/small/ , for example) and outputs. I have it for me, but it was written not very carefully and not committed.



