GSoC with flint: APR-CL primality test

Last couple weeks I added a lot of documentation, implemented important tests and fixed couple minor bugs, so this post is the summary for my implementation of primality test algorithm during GSoC with flint.

APR-CL is the mostly used algorithm for proving primality of general numbers. APR-CL (Adleman, Pomerance, Rumely, Cohen, Lenstra) is the modification of APR test. There are several versions of this algorithm and my implementation mostly described in [1] and [2]. Other modern tests are ECPP (Eliptice curve primality proving) and AKS (Agrawal–Kayal–Saxena).

APR-CL test uses the idea that we can not only check some conditions, but also collect this information and finally say that the number doesn't have any non trivial divisors. APR-CL uses the congruents analogues to Ferma's one. Finally, after we check some of these tests we can see that all possible divisor of n in small set of numbers, and to check that number is prime we only need "several" divisions ("several" can mean millions of divisions...but it's not very much for the numbers with thousands of digits). For more information see previous posts: (1), (2), (3).

My implementation is mostly based on [1]. I implemented a simple version that does not use $p-1$,  $p+1$ or Lucas style tests. While codeing I looked at PARI/GP and mpz_aprcl implementations and took some initial values (t's) from PARI.  After that I spent some time for "tuning" and now I believe that I chose a good values for numbers up to 2000 digits (but perhaps they can still be improved).

So, the algorithm consists from three steps:

• $R$ and $s$ selection
• Jacobi sum test
• Final division

As before, $n$ is the number to test for primality. We have $s$ such that $s^2 > n$ and $gcd(s*R, n) = 1$ and $a^R \equiv 1 \mod{s}$ for all $a$ coprime to $s$. Here we have 2 goals: minimize the $s$ and minimize the cost of future Jacobi sum test for $s$ divisors. I implemented only the first but the second also requires research (some ideas are described in [3]). Next we have final division step which depends from size of $R$ value. In final division we need to do $R$ divisions and it takes meaningful amount of time for big $n$.
$s$ reduction step described in this post. Also we can select $s^3 > n$, in all papers it was given as important improvement, but not implemented. Using flint implementation of Divisors in Residue Classes algorithm I have not get any speed gain for tested numbers. So I did not use it.

The essential part of Jacobi test step is to verify that power of multiplication of Jacobi sums is the unity root. So, the longest part of this step is exponentiation. As before we represent Jacobi sums as poly modulo cyclotomic poly, so we need to optimize modular polynomial exponentiation. This can be done in two directions: optimize powering function or polynomial multiplication/squaring functions. I worked on both of this and implemented 2^k-ry, sliding window exponentiation methods and special functions for multiplication and squaring.
In the future, this step can be improved if we add more special mul/sqr function (which, I believe, can be builded automatically, if we use some optimization methods..). Also before this step we can use Lucas style tests to look at some divisors and exclude them from Jacobi test. Finally, we can use some special forms of number to reduce the number of divisions (mod operations). For example, Montgomery form was implemented and tested, but it not give any speed up. I think it was mostly because I not implement it accuracy and better implementation can give some speed boost.
Some of these and other concepts are described [3].

In final step we just need to verify that n is prime. It was not very possible that we verify that n composite in this step, so it can't be used as effective factorization algorithm. In this step we know that all possible divisors of n can be find: if $s^2 > n$  then we check dividers in the form $n^i \mod{s}$; if $s^3 > n$ then we use Divisors in Residue Classes algorithm.

One of the easy and possible things to do is parallelization of second and third steps. I think it gave near linear speed up from number of processors, while we have only data ($q$ values in second and divisions in third) dependency which easy divides.

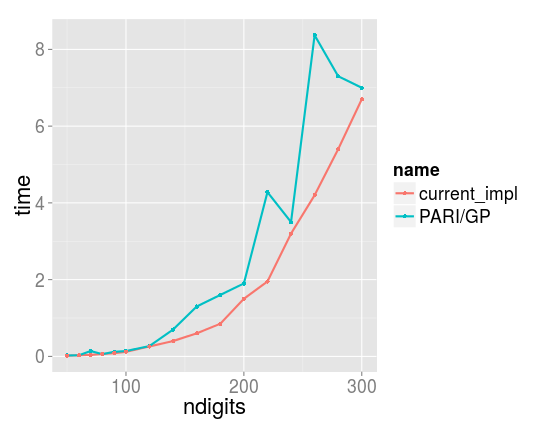
Finally I provide timings for current version. It can prove primality of 100 digit number for 0.7, 300 digit for 4 and 2000 digit for one hour on my 2.7 GHz Core i5 processor.

from 50 to 300 digit numbers

from 300 to 2000 digit numbers

So, I think it have good timings and believe it was many possible improvements. I hope my code was usefull for flint and merged after all necessary corrections.

Also provides Gauss sum test described in [4], which is not very useful in practice, but can beuseful for people who want to see an implementation of these.

Thanks flint and Google for this great summer of code!

[1] - "Implementation of a New Primality Test" by H. Cohen and A. K. Lenstra
[2] - "A Course in Computational Algebraic" by H. Cohen
[3] - "PRIMALITY PROVING WITH CYCLOTOMY" by Wiebren Bosma
[4] - "Four primality testing algorithms" by René Schoof

GSoC week 10; Some infrastructure code

This week I added a lot of comments and some documentation. Next I processed all compiler warnings and fix couple of bugs (in tests).

I created a new branch which contains all "clear" code (I remove Montgomery form and some extra files), so that we can review it and if everything is okay merge it..

timings from profiling code

I add profiling code with five primes of each size = 50, 60, ..., 300. I took a numbers from List of small primes. So anyone can now easily look at timings on his computer. I also run test for 2^2000+841 (603 digits) and 2^3515+159 (1059 digits) it took 60 and 700 seconds respectively.

In PARI/GP implementation for Jacobi sum computation them use q / 2 size table and I use two q size tables (to compute f(x) such that 1 - g^x = f(x), g - modulo q primitive root). Now I'm working on it. It will save a few megabytes of ram for large numbers and maybe give small speed up.

GSoC week 9; Special multiplication and s reduction

In the last week I tried a couple of interesting things, which well speed up the test.

I add config functions, which try to reduce $s$ value. If $s$ have prime power factor $q^k$ for which  $s/q^k > n^{1/2}$ then we can choose biggest $q$ and set $s = s/q^k$. This is repeated until it is no longer possible (_jacobi_config_reduce_s()). It gave a nice speed boost for numbers $n$ which are much smaller than the computed number $s$. This optimization enabled us to slightly outperform PARI/GP and "smooth" time of computation (no spikes).

up to 300 digits

Next following article, I have implemented the better $s$ reduction function (_jacobi_config_reduce_s2()) which is the approximation of knapsack problem solution. We choose weight of each $q$ equal to $w(q) = \sum\limits_{p | q-1}{\phi^2(p^j)}$, where $\phi$ denotes Euler's function.  Then we find a prime power factor $q^k$ of $s$ with max $w(q)$ and set $s = s/q^k$. By doing this as long as possible, we will get a good $s$ value. It also gave a small speed boost. For better explanations and links you can look at chapter 4 of "Primality Testing and Jacobi Sums". As I see it is not implemented in PARI/GP aprcl.

Another thing which gave interesting results - I remove $t = 166320 = 2^4*3^3*5*7*11$ and always use $t = 720720 = 2^4*3^2*5*7*11*13$. If we use it together with $s$ reduction function we have ~0.5 second speed up for 300 digits prime (5.6 sec instead of 6.1). These is because we do not have a special sqr/mul functions for p = 13 or p = 27, but for p = 27 we have poly of length 17 and for p = 13 length = 12. After using $s$ reduction function in both cases we have $s$ of similar size, but use faster multiplication/squaring. It works for all numbers which are used t = 166320. Also in this place there is space for optimization, because now in final divison step we need to do 720720 multiplications and divisions, and it takes ~15% of all time.

The next thing to look at in the future is special functions sqr/mul for all $p$ values. I look at p = 13 and write result for squaring and I don't think that's a good idea to work with it manually. It look like some type of cse task and I think I can find some algorithm for this later...

I also add special multiplication functions for p = 3, 4, 5, 7, 8, 9, 11 and 16. It gave just a couple of percent increase, but almost for free :)

So, now test works 0.115 sec for 100 and 5.6 sec for 300 digits numbers (I think I have never posted my processor type - Core2Duo T6670 2.2GHz processor, so I do not have avx instructuions set, which may be can be used in gmp).

This week I want to fix all warnings I have, do some refactoring and add more documentation. I also want to add something similar to profile folder with primes of different sizes (from https://primes.utm.edu/lists/small/ , for example) and outputs. I have it for me, but it was written not very carefully and not committed.

GSoC week 8; More squaring functions

This week not much has changed, but I tried a couple of things that gave nothing.

After using Montgomery form for general multiplication and squaring I try to use it in special sqr functions (like unity_zp_sqr7). For this I add some modular functions for fmpz in Montgomery form (add, sub, mul: inlined in aprcl.h file) and add unity_zp_mont_sqr7() function. Using it instead of unity_zp_sqr7 and simple form works slower. Maybe, I implement something not very accurately.

I also add unity_zp_sqr11() function and it gave a good speed up (~10% for 300 digits number; we can test 300 digits $n$ for 7.3 sec). Functions like this give a better performance, but them require a lot time to code and debug. So far I have used the Supplement to Implementation of a New Primality Test, but the better way is to think about generalization.

from 50 to 100 digits

from 50 to 300 digits

On the other hand if I add similar functions for $p^k = 13, 27, 32$ this will be enough for the numbers up to ~1000 of digits. I also need to have a better look at $R$ and $s$ selection.

I think that I need to rewrite unity_zp_sqr and unity_zp_mul functions to reduce modulo $n$ after cyclotomic poly reduction, so we have less number of fmpz_mod function calls. 
Only 4 weeks left until soft GSoC deadline, so I have to start thinking about future code integration (as first step I want to create new branch and remove files related with Gauss sum test).

Valgrind callgrind call graphs for 100 and 300 digits numbers.

GSoC week 7; Montgomery modular stuff

This week I add squaring for p = 16 and it give good speed up for 100 digit prime (actually, for ~100 digit number used my implementations of squaring). After this we can prove 100 digit number primality for 0.13 sec and 300 digit number for 8.3 sec.

The next thing I was working on is Montgomery modular multiplication and reduction.
Firstly, we need to convert our unity_zp structure (recall that it is just a fmpz_mod_poly, mod = n) into Montgomery. For this we need to select $r > n$ such that $r = 2^k$ and compute $f * r$ there $f$ - unity_zp; so, element $x$ in Montgomery form can be represented as $x = a * r$, there $a$ from simple form. Because we do not want to use fmpz_mod or division functions we can store our unity_zp_mont data into fmpz_poly.  It was implemented in unity_zp_mont_to() and init functions.

Secondly, we need to implement basic operations. Addition and subtraction are the same as ordinary modular addition and subtraction: $x + y = a*r + b*r = (a + b)r = z$ there $x$, $y$ and $z$ in Montgomery form. Multiplications works a little harder: $x * y = (a*r) * (b*r) = (a*b)*r^2$, so we need to divide by $r$. To do it fast exists special REDC function, which uses the fact that $r = 2^k$ and we can use binary shift operations instead of division.

Using this form in exponentiation function gives small speed up (8 sec instead of 8.3 for 300 digits number). I think, if I implement REDC function in lower level (GMP have some implementations, but them not have public interface) this will give even a small increase in speed. Moreover, I not use REDC for small p = 4, 5, 7, 9 and 16, so Montgomery stuff not used for small numbers.

GSoC week 6; Midterm and more optimizations

This week I refactor powering algorithms and add sliding window exponentiation implementation. It gave speed boost in couple of percent.

The next thing I do is add special squaring functions for small p values: powers of 2 (for 4 and 8); 3; 5; 7 (for details see the "Implementation of a New Primality Test" supplement). Selection of function going on unity_zp_sqr_inplace() and we need to have allocated memory for fmpz_t array (t).

It gives good speed boost (~10-15%), and for "small" numbers (near 100 digits) we catch up the PARI/GP implementation and I'm confident that we will soon become faster. For bigger values PARI/GP is still faster. Below the graphs with timings up to 100 and 300 digits:

50-100 digits

50-300 digits

I also looked at $(n - 1)$ test to replace computation in $\mathbb{Z}[\zeta_r]/(n)$ by $\mathbb{Z}/n\mathbb{Z}$, but I don't see that it will give a good speed gain.
Now I want to try reduce s value for fixed R (as in (4.) of "Primality Testing and Jacobi Sums"). After we compute s we can try to remove some factors without which we still have $s^2 > n$.

In total, over the past six weeks has been implemented APR-CL algorithm with good performance. Almost all of code is tested and documented. So now I need to finish special cases of multiplication and squaring and then try to optimize in general. Also we need to look closely at different initial values of R because the values from PARI/GP impair the performance (look at 70 digit numbers in first plot, for example).

GSoC week 5; Some optimizations

This week I was working on the Jacobi sum test optimizations described in the last post.
First I add some fixed optimal $R$ values for $n$ with different number of digits. I also rewrite $s$ computation. This functions can be find here. It gave a good gain in speed, but I can add more intermediate $R$ values. It must be done carefully, because with smaller $R$ we can have worse $s$. This is shown in the graph, the PARI/GP implementation has many peaks.

mean time in seconds

Next I add $2^k$-ary powering algorithm. It gave ~20% gain in speed.

Also I do a lot of profiling using valgrind callgrind tool. I find that the computation of Jacobi sums takes a little time, so I'm not going to tabulate them.

I implement the final step of algorithm on condition that $s^3 > n$ using divisors in residue classes algorithm. After that all becomes slower. The divisors in residue classes algorithm have a good complexity $O((\ln n)^3$, but we need to call it thousands of times ($R = 2520$ for 100 digits $n$).

The next graph show timings for $n$ from 50 to 100 digits:

mean time in seconds

To better understand how selection of $R$ affects at the time I look at most slow part of algorithm ($n$-th powering in $\mathbb{Z}[\zeta_r] / (n)$) and count the number of operations. This can be seen in the following tables for 100 and 300 digits numbers: 
  
Also attach link to valgrind outputs for 100 and 300 digits prime. 

Next I want try to use directly fmpz_vec operations, without fmpz_mod_poly abstraction. After this I want to implement some formulas described in "Implementation of a New Primality Test" for fixed $r = p^k$.